ত্রিকোণমিতিক সূত্রাবলি – HSC গণিত
ত্রিকোণমিতি (Trigonometry) গণিতের একটি গুরুত্বপূর্ণ ও আকর্ষণীয় শাখা। এই অধ্যায়টি ভালভাবে আয়ত্ত করতে পারলে, Higher Math ও বাস্তব জীবনের বিভিন্ন সমস্যা সমাধানে সহজ হবে। নিচে ধাপে ধাপে সব গুরুত্বপূর্ণ সূত্র, উদাহরণ ও প্রয়োগ আলোচনা করা হলো।
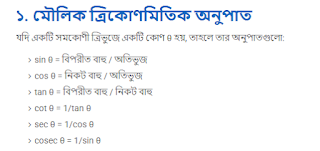
মৌলিক ত্রিকোণমিতিক অনুপাত
- sin θ = বিপরীত বাহু / অতিভুজ
- cos θ = নিকট বাহু / অতিভুজ
- tan θ = বিপরীত বাহু / নিকট বাহু
- cot θ = 1 / tan θ
- sec θ = 1 / cos θ
- cosec θ = 1 / sin θ
মৌলিক পরিচিতি (Fundamental Identities)
| সূত্র | ব্যাখ্যা |
|---|---|
| sin²θ + cos²θ = 1 | ত্রিভুজের মৌলিক সম্পর্ক |
| 1 + tan²θ = sec²θ | tan ও sec এর সম্পর্ক |
| 1 + cot²θ = cosec²θ | cot ও cosec এর সম্পর্ক |
দ্বিগুণ কোণের সূত্র (Double Angle Formulas)
- sin(2θ) = 2sinθ·cosθ
- cos(2θ) = cos²θ − sin²θ = 2cos²θ − 1 = 1 − 2sin²θ
- tan(2θ) = (2tanθ) / (1 − tan²θ)
বিস্তারিত রূপগুলো:
- sin(2A) = 2sinA·cosA
- cos(2A) = cos²A − sin²A
- cos(2A) = 2cos²A − 1
- cos(2A) = 1 − 2sin²A
- tan(2A) = (2tanA) / (1 − tan²A)
যোগ ও বিয়োগ সূত্র
- sin(A ± B) = sinA·cosB ± cosA·sinB
- cos(A ± B) = cosA·cosB ∓ sinA·sinB
- tan(A ± B) = (tanA ± tanB)/(1 ∓ tanA·tanB)
অর্ধ কোণের সূত্র (Half Angle Formulas)
- sin²θ = (1 − cos(2θ))/2
- cos²θ = (1 + cos(2θ))/2
- tan²θ = (1 − cos(2θ))/(1 + cos(2θ))
গুণ থেকে যোগফল এবং যোগ থেকে গুণ সূত্র:
যোগফল থেকে গুণ সূত্র:
- sinA + sinB = 2sin[(A + B)/2]·cos[(A − B)/2]
- sinA − sinB = 2cos[(A + B)/2]·sin[(A − B)/2]
- cosA + cosB = 2cos[(A + B)/2]·cos[(A − B)/2]
- cosA − cosB = −2sin[(A + B)/2]·sin[(A − B)/2]
গুণ থেকে যোগফল সূত্র:
- 2sinA·cosB = sin(A + B) + sin(A − B)
- 2cosA·sinB = sin(A + B) − sin(A − B)
- 2cosA·cosB = cos(A + B) + cos(A − B)
- 2sinA·sinB = cos(A − B) − cos(A + B)
ত্রিগুণ কোণের সূত্র (Triple Angle Formulas)
sin(3θ) সূত্র
সূত্র: sin(3θ) = 3sinθ − 4sin³θ
উদাহরণ: যদি θ = 30°, তাহলে
sin(3×30°) = sin(90°) = 1
আর, 3sin(30°) − 4sin³(30°) = 3×0.5 − 4×(0.5)³ = 1.5 − 0.5 = 1
✅ উভয় পদ্ধতিতে একই ফলাফল
cos(3θ) সূত্র
সূত্র: cos(3θ) = 4cos³θ − 3cosθ
উদাহরণ: যদি θ = 60°, তাহলে
cos(3×60°) = cos(180°) = −1
আর, 4cos³(60°) − 3cos(60°) = 4×(0.5)³ − 3×0.5 = 0.5 − 1.5 = −1
✅ উভয় পদ্ধতিতে একই ফলাফল
tan(3θ) সূত্র
সূত্র: tan(3θ) = (3tanθ − tan³θ)/(1 − 3tan²θ)
উদাহরণ: যদি θ = 15°, তাহলে
tan(3×15°) = tan(45°) = 1
এখন, tan(15°) ≈ 0.2679
তাহলে:
উপর = 3×0.2679 − (0.2679)³ ≈ 0.8037 − 0.0192 ≈ 0.7845
নিচ = 1 − 3×(0.2679)² ≈ 1 − 3×0.0718 ≈ 1 − 0.2154 ≈ 0.7846
tan(3θ) ≈ 0.7845 / 0.7846 ≈ 1
✅ ফলাফল মিলে গেছে
সংক্ষেপে সব সূত্র:
- sin(3θ) = 3sinθ − 4sin³θ
- cos(3θ) = 4cos³θ − 3cosθ
- tan(3θ) = (3tanθ − tan³θ) / (1 − 3tan²θ)
প্রয়োগ ও উদাহরণ
📌 উদাহরণ ১: প্রমাণ করুন যে tan²A + 1 = sec²A
সমাধান: tan²A + 1 = (sin²A / cos²A) + 1 = (sin²A + cos²A)/cos²A = 1/cos²A = sec²A
📌 উদাহরণ ২: প্রমাণ করুন, sin²x + cos²x = 1
সমাধান: এটি মৌলিক সূত্র, যেকোনো কোণের জন্য প্রযোজ্য।
📌 উদাহরণ ৩: প্রমাণ করুন, 1 + cot²A = cosec²A
সমাধান: cot²A + 1 = (cos²A/sin²A) + 1 = (cos²A + sin²A)/sin²A = 1/sin²A = cosec²A
অনুশীলনী প্রশ্ন (Practice)
- প্রশ্ন ১: প্রমাণ করুন যে, sec²x − tan²x = 1
- প্রশ্ন ২: sin3x এবং cos3x এর জন্য triple angle formula লিখুন।
- প্রশ্ন ৩: sinA = 3/5 হলে, cosA ও tanA নির্ণয় করুন।
বিপরীত ত্রিকোণমিতির সূত্র (Inverse Trigonometric Formulas)
বিপরীত ত্রিকোণমিতি: যদি sin θ = x হয়, তাহলে θ = sin⁻¹(x) হয়। একে বিপরীত ত্রিকোণমিতি বলা হয়। একইভাবে cos⁻¹(x), tan⁻¹(x) ইত্যাদি রয়েছে।
মৌলিক বিপরীত ত্রিকোণমিতি সূত্র:
- sin⁻¹(x) = θ ⇔ sin(θ) = x, যেখানে −1 ≤ x ≤ 1
- cos⁻¹(x) = θ ⇔ cos(θ) = x, যেখানে −1 ≤ x ≤ 1
- tan⁻¹(x) = θ ⇔ tan(θ) = x, যেখানে −∞ < x < ∞
- cot⁻¹(x) = θ ⇔ cot(θ) = x
- sec⁻¹(x) = θ ⇔ sec(θ) = x, যেখানে |x| ≥ 1
- cosec⁻¹(x) = θ ⇔ cosec(θ) = x, যেখানে |x| ≥ 1
বিপরীত ত্রিকোণমিতি ফাংশনের সম্পর্ক:
- sin⁻¹(x) + cos⁻¹(x) = π/2
- tan⁻¹(x) + cot⁻¹(x) = π/2
- sec⁻¹(x) + cosec⁻¹(x) = π/2
বিপরীত ত্রিকোণমিতির পারস্পরিক রূপান্তর:
- sin⁻¹(x) = tan⁻¹(x / √(1 - x²)), যখন -1 < x < 1
- cos⁻¹(x) = tan⁻¹(√(1 - x²) / x), যখন 0 < x ≤ 1
- tan⁻¹(x) = sin⁻¹(x / √(1 + x²))
বিপরীত ত্রিকোণমিতির যৌগ সূত্র:
- tan⁻¹(x) + tan⁻¹(y) = tan⁻¹((x + y) / (1 - xy)), যখন xy > 1
- tan⁻¹(x) - tan⁻¹(y) = tan⁻¹((x - y) / (1 + xy)), যখন xy < 1
কিছু গুরুত্বপূর্ণ মান:
| ফাংশন | মান |
|---|---|
| sin⁻¹(0) | 0 |
| sin⁻¹(1) | π/2 |
| cos⁻¹(0) | π/2 |
| cos⁻¹(1) | 0 |
| tan⁻¹(1) | π/4 |
উদাহরণ:
উদাহরণ ১: sin⁻¹(1/2) এর মান নির্ণয় করুন।
সমাধান: sin(π/6) = 1/2 ⇒ sin⁻¹(1/2) = π/6
উদাহরণ ২: tan⁻¹(1) + cot⁻¹(1) = ?
সমাধান: tan⁻¹(1) = π/4 এবং cot⁻¹(1) = π/4 ⇒ যোগফল = π/2
উদাহরণ ৩: sin⁻¹(x) + cos⁻¹(x) = ?
সমাধান: sin⁻¹(x) + cos⁻¹(x) = π/2 (যেকোনো x এর জন্য, যেখানে −1 ≤ x ≤ 1)
শেষ কথা
ত্রিকোণমিতিক সূত্রগুলো শুধু মুখস্থ করলেই হবে না, বরং প্রতিটি সূত্র কীভাবে ব্যবহার করতে হয় তা অনুশীলনের মাধ্যমে বুঝে নিতে হবে। Mathcheap সব সময় শিক্ষার্থীদের জন্য সহজ ভাষায় গণিত শেখানোর চেষ্টা করে যাচ্ছে।
পোস্টটি ভালো লাগলে শেয়ার করতে ভুলবেন না। আপনার মতামত বা প্রশ্ন নিচের কমেন্টে জানান।
লেখক পরিচিতি:
আরিফিন আকাশ
প্রভাষক(গণিত) ও Mathcheap এর স্বত্বাধিকারী
গণিত, বিজ্ঞান, ও প্রযুক্তি বিষয়ক লেখক।
ওয়েবসাইট: www.mathcheap.com
Facebook: facebook.com/mathcheap